CCK-CBS
We adapt K-CBS for chance-constrained multi-robot motion planning (CC-MRMP) where the robots are subject to both process and measurement noise.
Motion planning under Gaussian uncertainty has largely been studied for single-robot systems. The most efficient algorithms are sampling-based planners, which are analogous to their deterministic counterparts, e.g., feedback-based information roadmaps and rapidly-exploring random belief trees. The Belief-A framework provides a generic structure for adapting any sampling-based kinodynamic planner Belief-A into a belief space planner. Fast planning is possible by using a chance constraint formulation of collision avoidance. Although these approaches can solve uncertain motion planning, they cannot handle uncertain MRMP out of the box.
One approach to uncertain MRMP is to abstract the problem to a multi-agent Markov Decision Process (MMDP), then reduce to single-agent MDPs with a joint action space. This relies on abstraction of the robot dynamics to a discretized transition probability matrix, which is difficult and scales poorly to many robots. Additionally, MMDPs solely account for uncertain dynamics, whereas measurement noise requires using a Partially Observable MDP (POMDP), which can be very difficult to solve and also scales poorly. Other uncertain MRMP approaches use online distributed planning, where each robot plans over a short horizon to account for nearby robots and obstacles. These methods perform well in unknown environments. However, neither POMDP approaches nor online distributed methods provide any formal performance or completeness guarantees.
We address this gap by presenting a scalable MRMP algorithm for robots operating with Gaussian state and measurement noise. We combine the scalability of K-CBS with the fast belief-space planning of Belief-A to solve MRMP for robots under Gaussian uncertainty. While keeping the architecture of both algorithms intact, our main contribution is extending the validity checking capabilities of K-CBS to account for chance-constrained robot-robot collisions. Our algorithm, Chance-Constrained K-CBS (CCK-CBS), is probabilistically complete via the completeness inheritance properties of K-CBS and Belief-A. Some examples plans (with noisy simulation data) from CCK-CBS are shown below.

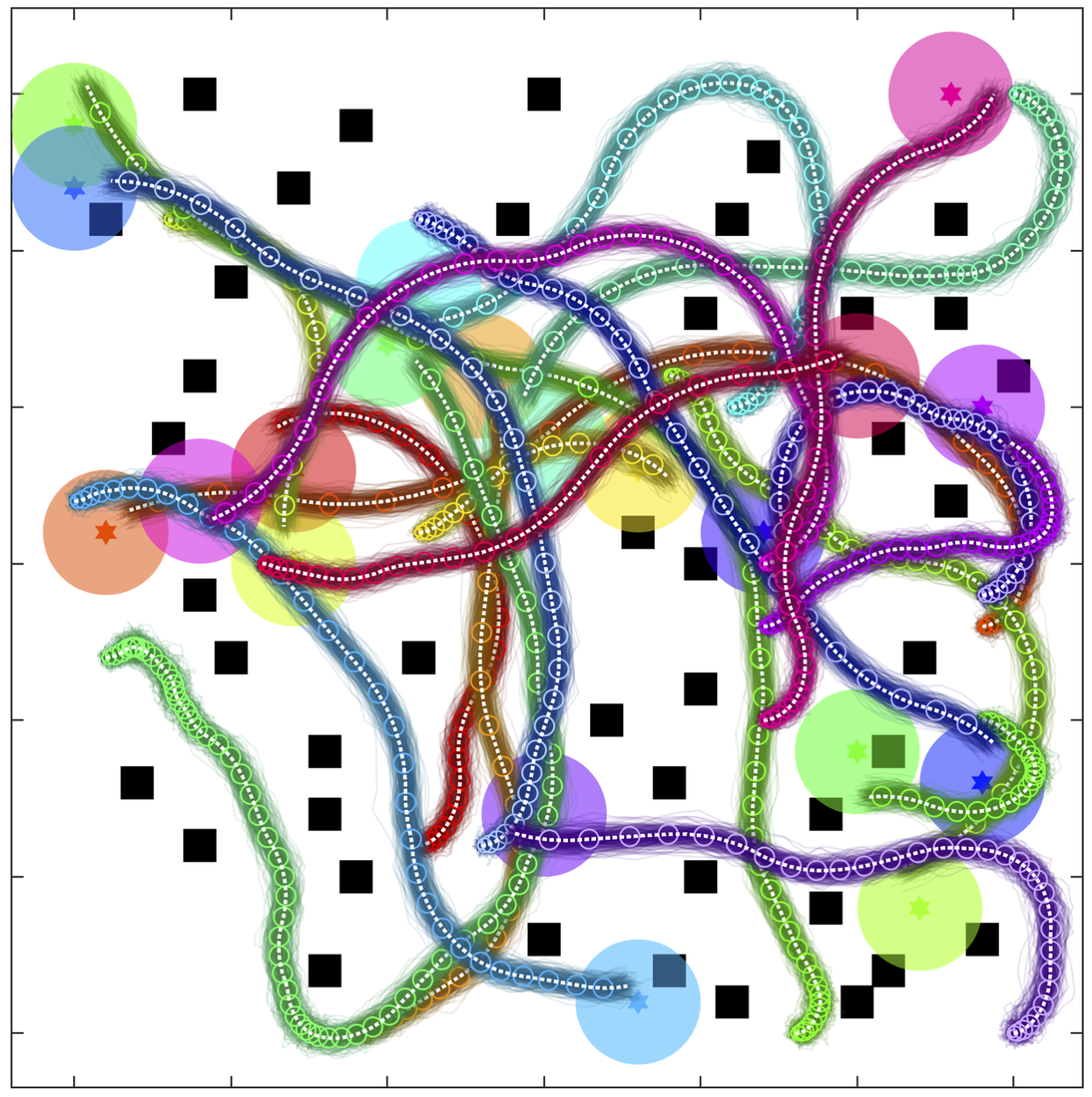

I invite you to investigate any of these great resources to learn more about CCK-CBS:
- The original CCK-CBS RAL 2023 Letter Paper
- The implementation of CCK-CBS