K-CBS

Kinodynamic Conflict-Based Search (K-CBS) is a complete and scalable MRMP algorithm.

Multi-robot motion planning (MRMP) is the fundamental problem of finding non-colliding trajectories for multiple robots acting in an environment, under kinodynamic constraints. Due to its complexity, existing algorithms utilize simplifying assumptions, are incomplete, or both. To this end, this work introduces a decoupled, scalable, and (proabilistically) complete MRMP algorithm that treats the kinodynamic constraints of the robots natively. Unlike related works that directly adopt MAPF algorithms on a discretized version of the problem, we incorporate the ideas that make CBS successful into the continuous domain using a sampling-based method. Our algorithm, dubbed Kinodynamic CBS (K-CBS), like CBS, uses a low-level search and maintains a constraint tree. The low-level search can be any (kinodynamic) sampling-based tree planner (e.g., RRT or KPIECE).

Many conflicts occur during a single collision between the orange and blue robots within the collision time-interval. The set of conflicts creates one constraint for each robot, which are reasoned about separately. Constraint on orange agent is not shown.

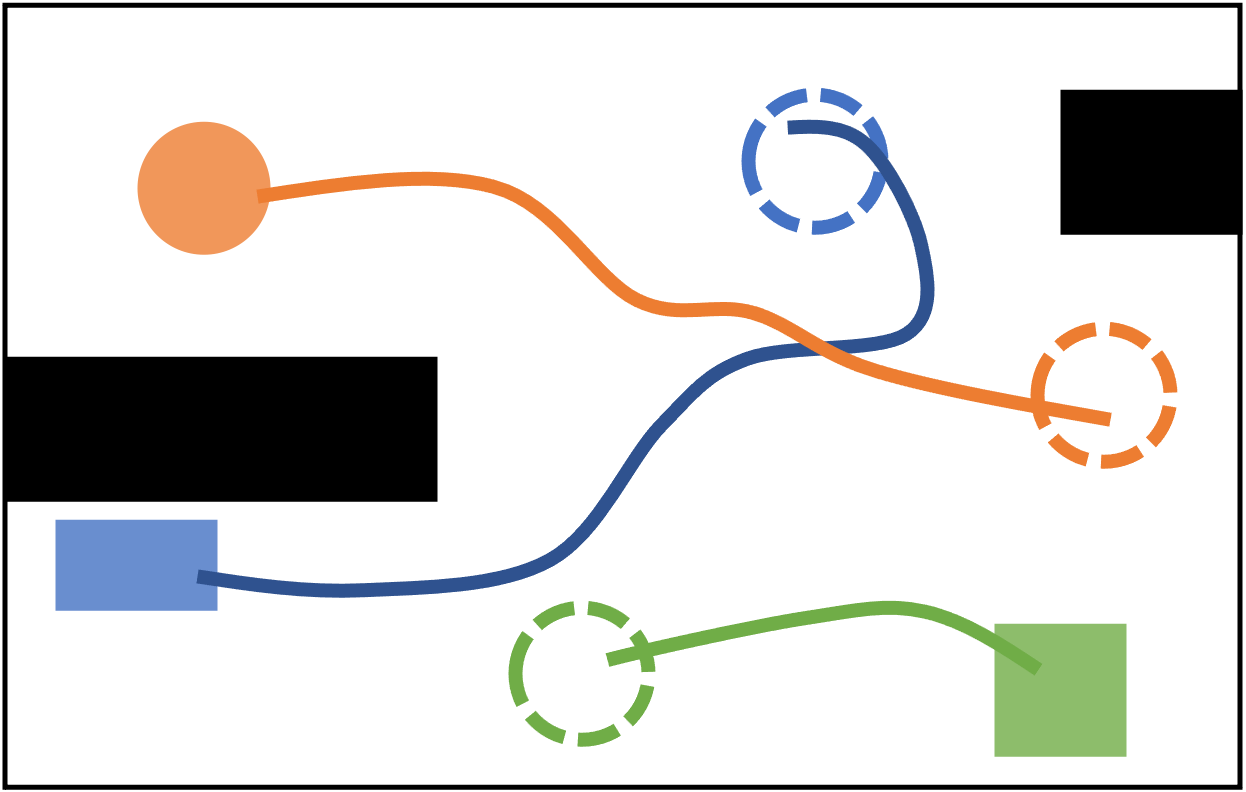
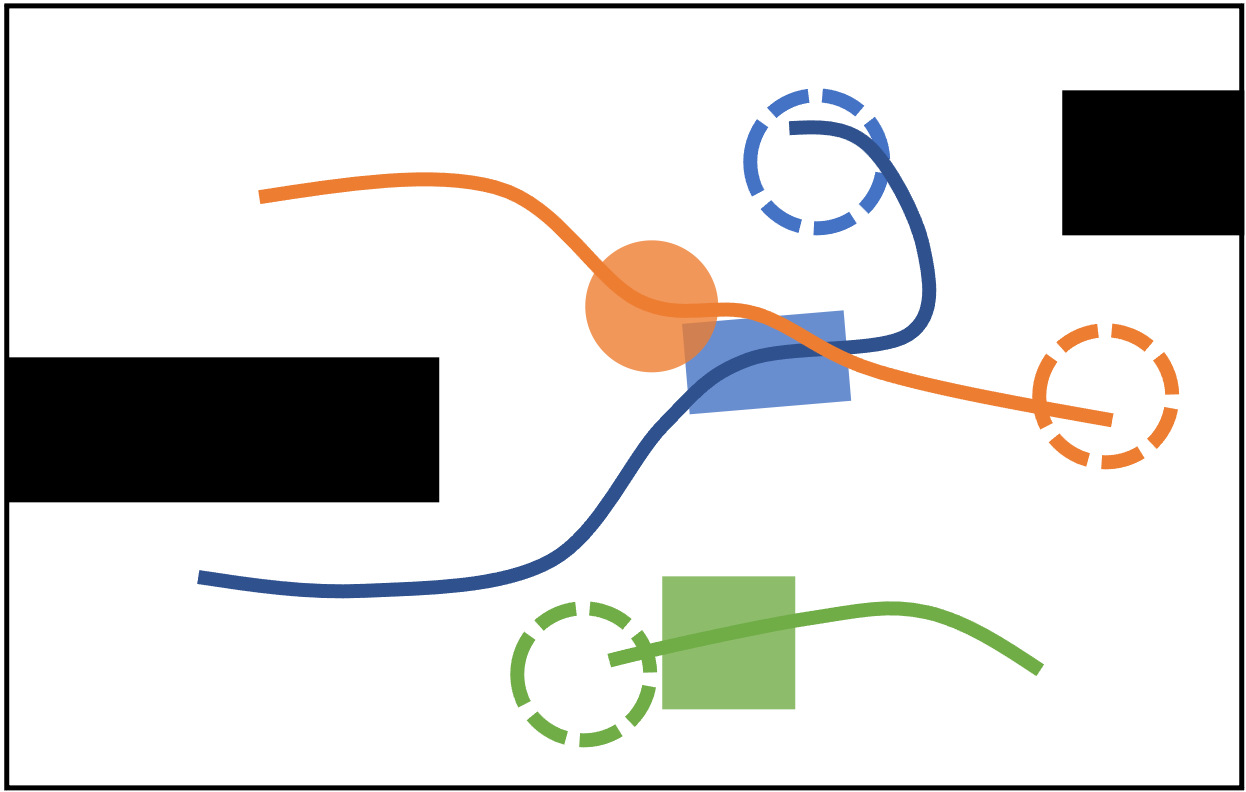
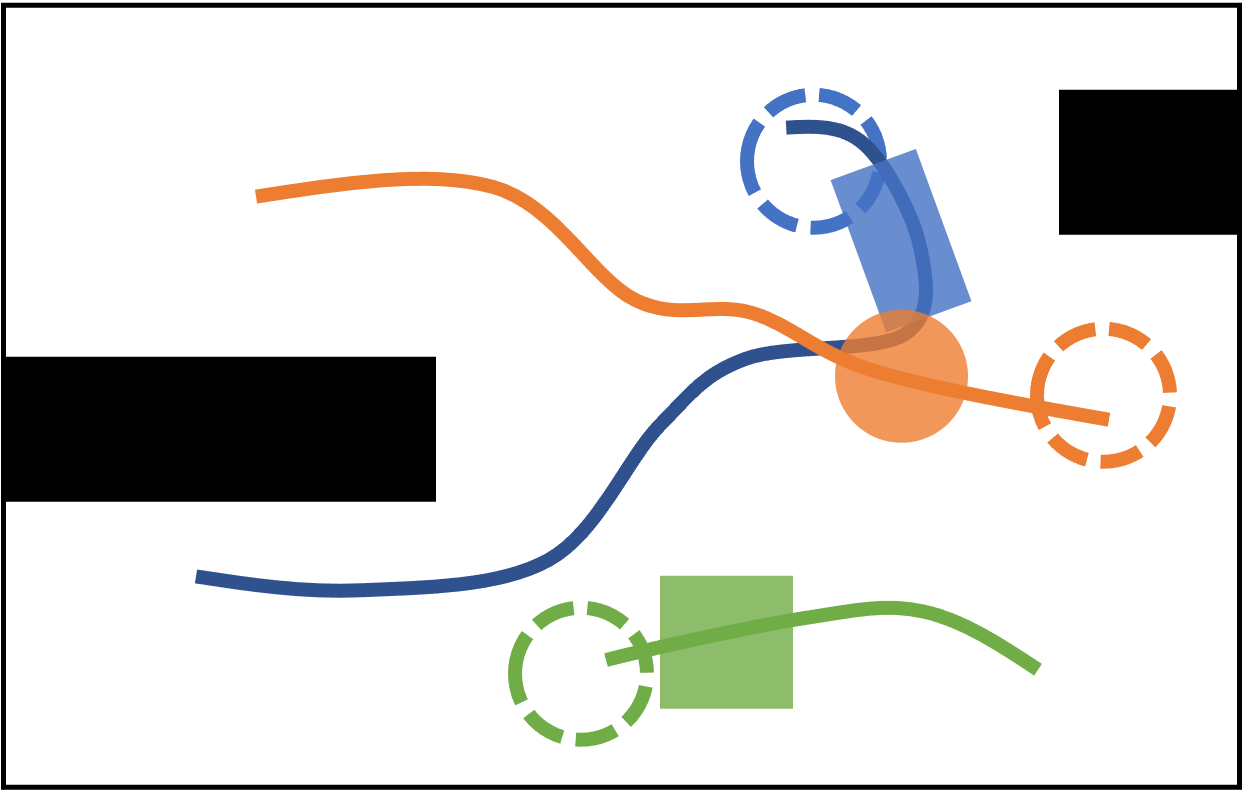
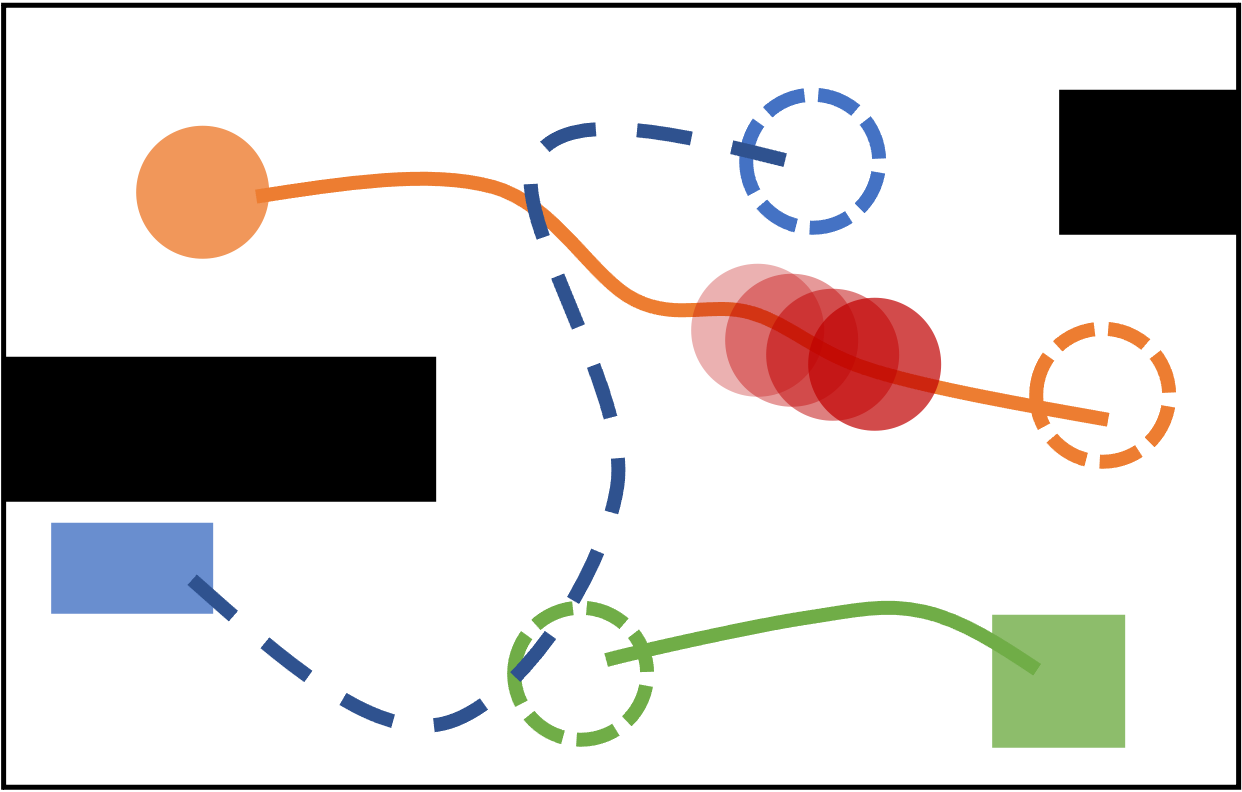
In each iteration of K-CBS, a trajectory is computed for an individual robot given a set of constraints (time-dependent obstacles). Then, collisions between the robot trajectories are checked. If one exists, constraints are defined in the constraint tree, and a new planning query is specified accordingly. To ensure probabilistic completeness, we introduce a \emph{merge and restart} method, by which we merge robots whose plans often conflict, into a single meta-robot.

The main contribution of this work is a decoupled, probabilistically-complete MRMP algorithm that is capable of generating kinodynamically feasible plans efficiently. Our algorithm, K-CBS, naturally adapts CBS from MAPF to MRMP. This lifts every off-the-shelf (kinodynamic) random tree-based planner to the multi-robot setting and removes all the limitations (assumptions) of state-of-the-art MRMP planners. Specifically, K-CBS operates completely in the continuous state space of the agents, hence, it does not require discretization nor a feedback-control design. It easily works with arbitrary, possibly heterogeneous, nonlinear dynamical models, and is capable of solving very complex MRMP instances efficiently. Some example solutions are shown below.

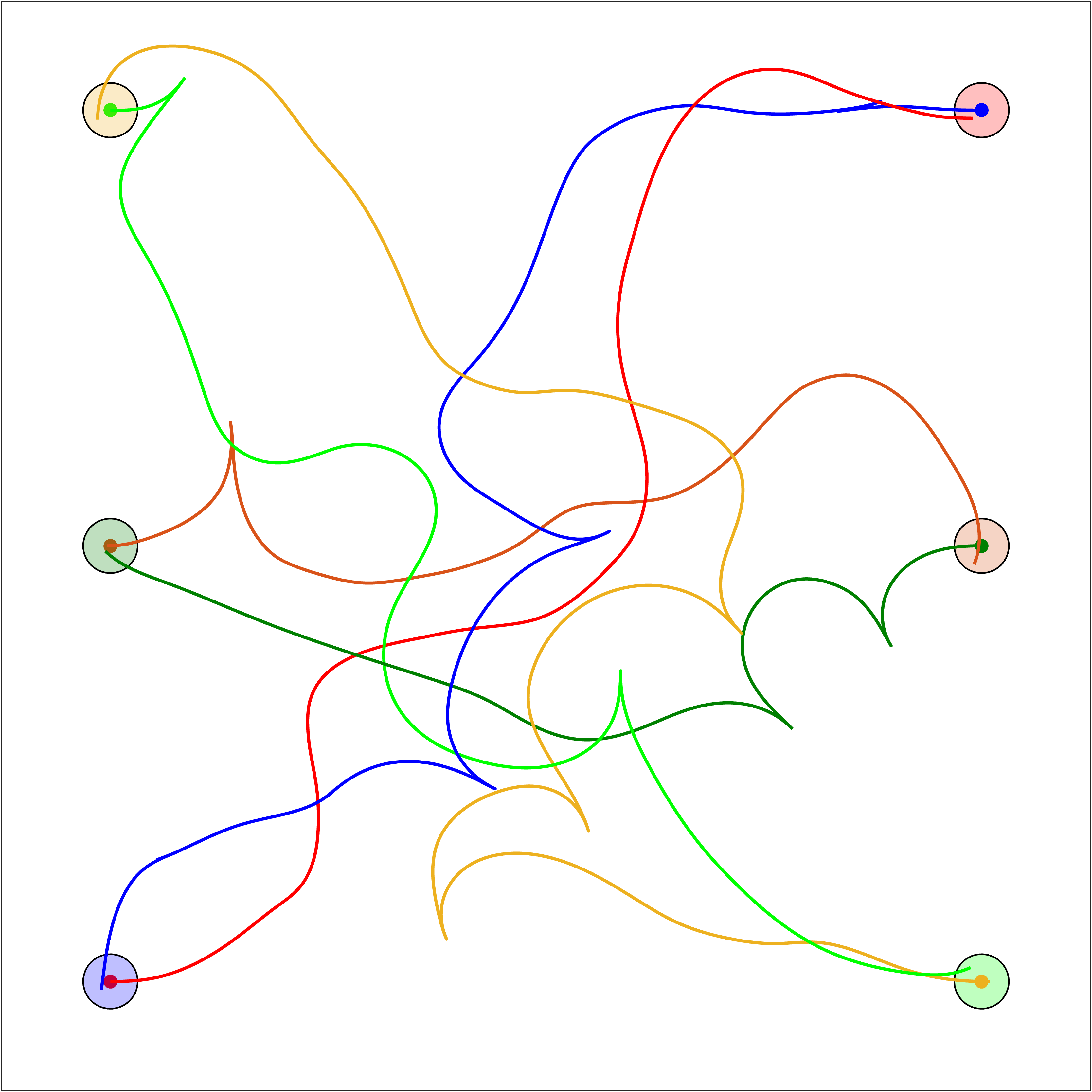
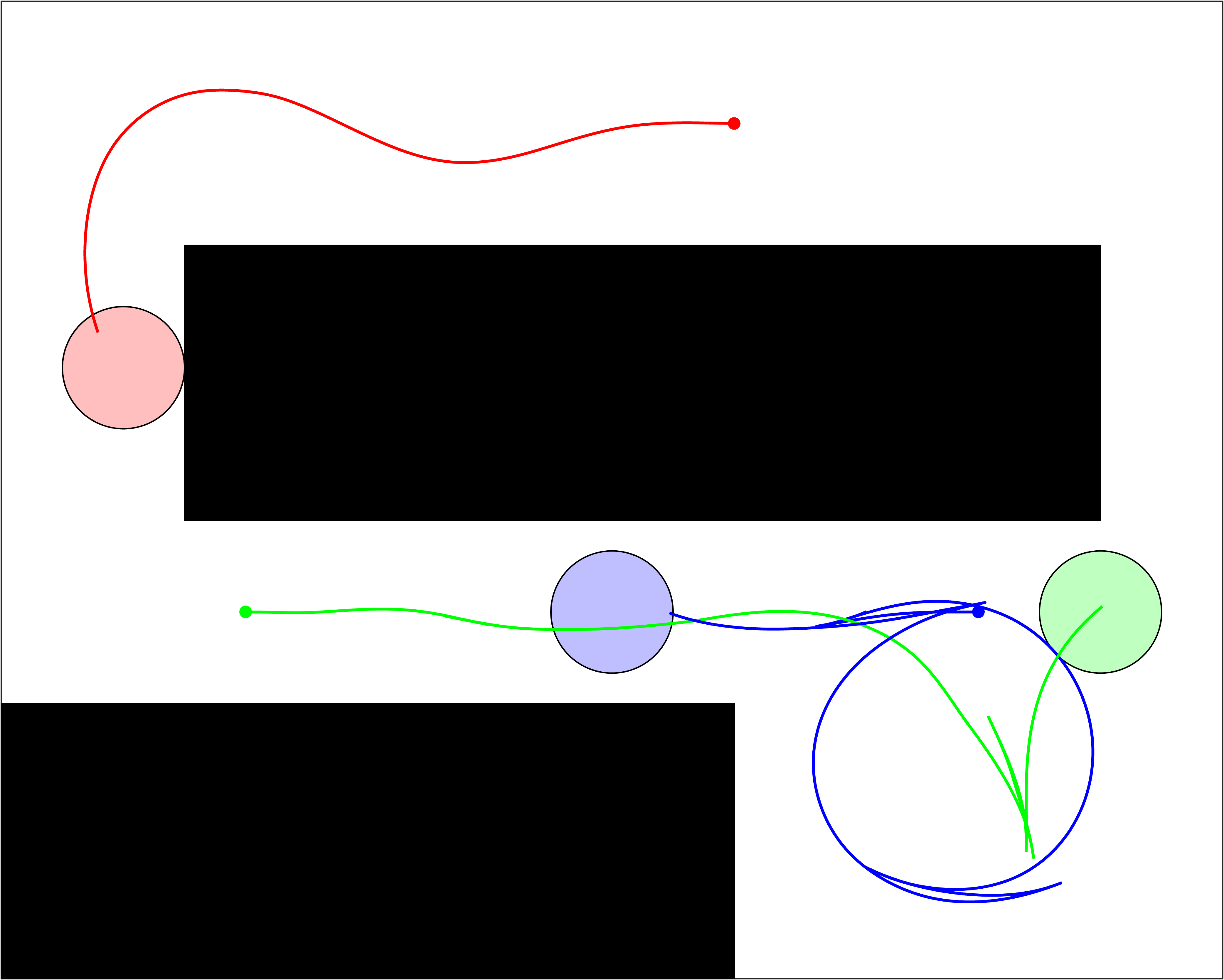
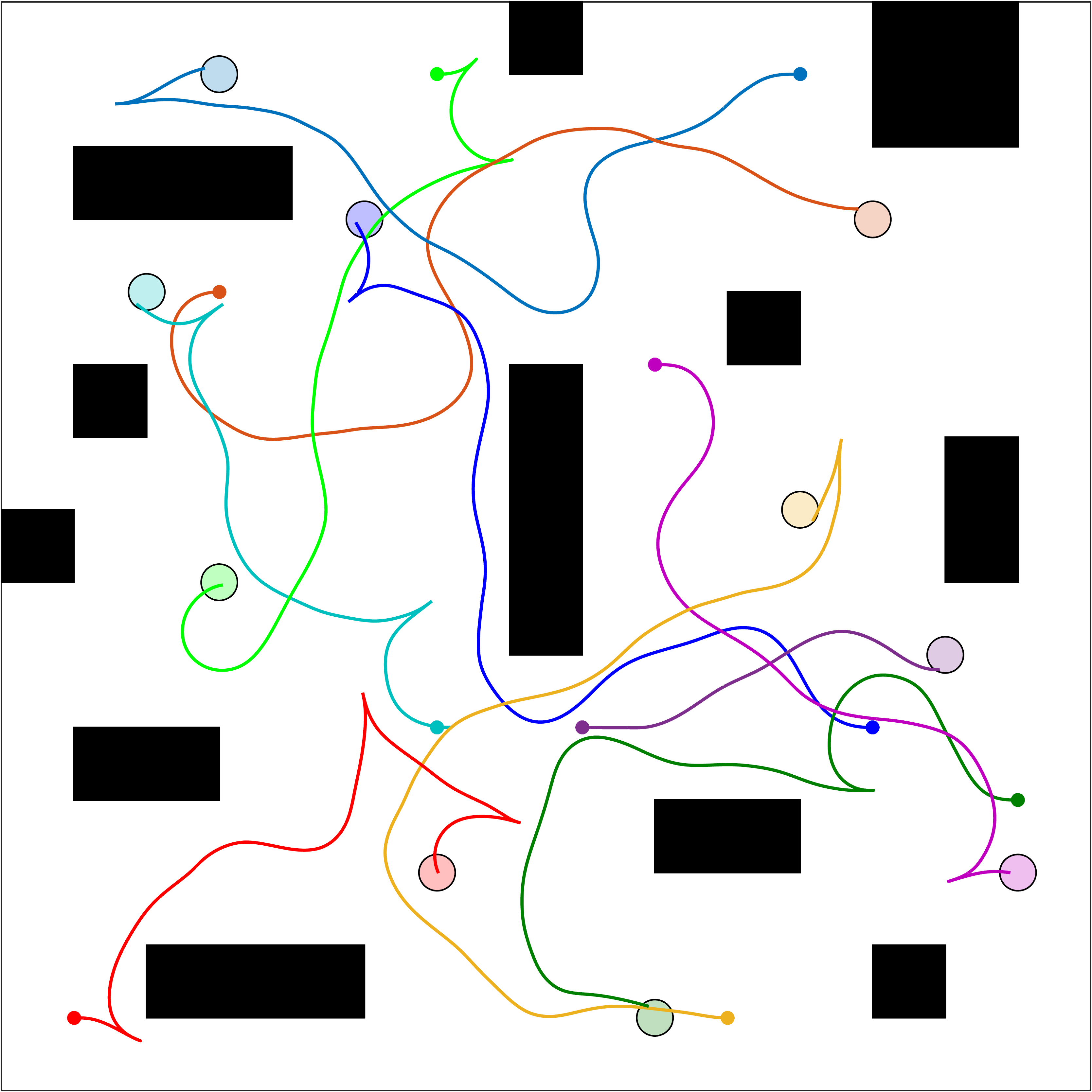
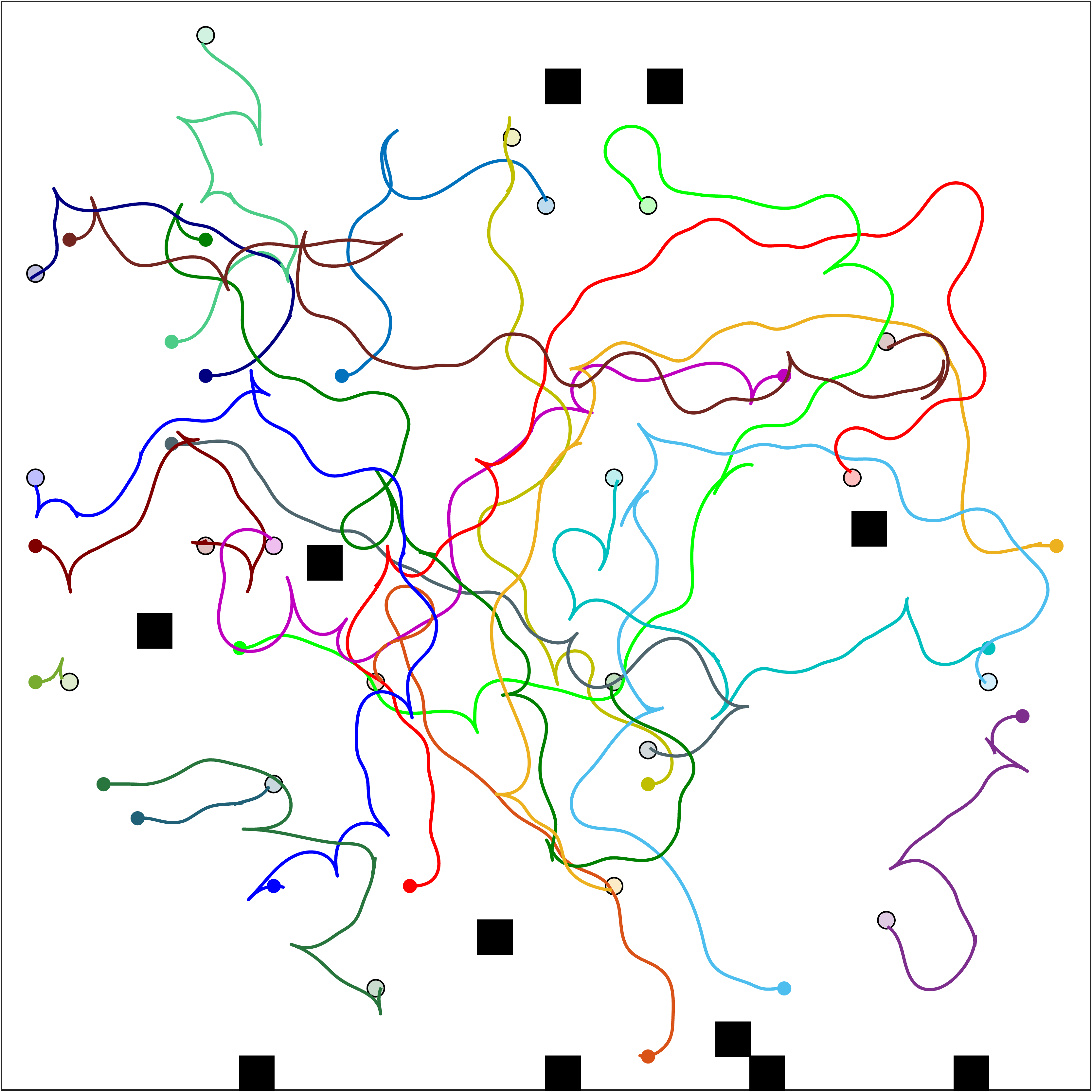
Solved MRMP instances using K-CBS. The initial states are shown with small circles and goal regions with large circles. K-CBS calculates plans in all of these spaces with great success without any limiting assumptions on the MRMP problem.

I invite you to investigate any of these great resources to learn more about K-CBS:

  1. The original K-CBS IROS 2022 Conference Paper
  2. The most-current implementation of K-CBS (to my knowledge) located inside The Multi-Robot OMPL Repository
  3. The extended K-CBS Demos Repository that pairs with the MR-OMPL implementation